zzq 题目选做

真 成 🤡 了 ！

洛谷 P3672 小清新签到题

拿到这个题后发现只能想到计数来构造，好像没有其他方法喵~。😿

考虑设一个最暴力的 $dp$，设 $f_{i,j}$ 表示考虑一个长度为 $i$ 的排列，有 $j$ 个逆序对的方案数，因为我们填排列是从前往后填数，所以 $dp$ 应该从后往前转移，这样在我考虑第 $i$ 位时我能快速知道第 $i$ 位填 $x$ ，后面随便填时有多少排列，转移也很朴素，$f_{i,j}=\sum\limits_{k=1}^{i}f_{i+1,j-k+1}$，其实就是我枚举第一个数是什么，直接转移。

这个 $dp$ 状态是 $O(n^3)$ 的，转移是 $O(n)$ 的，寄，但是显然转移的复杂度很容易用前缀和优化成 $O(1)$，这样就行了。

现在考虑求出了这个 $dp$ 数组有什么用，其实我就直接按照题意走一个类似数位 $dp$ 的东西就行了。

具体来说，假设我考虑到第 $i$ 位，枚举第 $i$ 位的数在后 $n-i$ 个数的排名 $val$，找到第一个满足 $\sum\limits_{j=1}^{val} f_{i+1,x-j+1} \ge k$ 的值，其中的 $x,k$ 都是题目中给的， 让后让 $x$ 减去 $val-1$，让 $k$ 减去 $\sum\limits_{j=1}^{val-1} f_{i+1,x-j+1}$，重复操作继续做下一位。

code:

typedef long long LL;
const int N=307;
const LL INF=1e13;
int n,K; LL m;
LL f[N][N*N/2],sum[N*N/2];
int a[N];
int main(){
	rd(n,m,K);
	f[0][0]=1;
	for(int i=1;i<n;i++){
		sum[0]=f[i-1][0];
		for(int j=1;j<=min(K,i*(i-1)/2);j++) sum[j]=min(INF*j,sum[j-1]+f[i-1][j]);
		for(int j=0;j<=min(K,i*(i-1)/2);j++) f[i][j]=min(INF,sum[j]-(j-i>=0?sum[j-i]:0));
	}
	for(int i=n;i>=1;i--){
		LL sum=0;
		for(int j=0;j<i&&j<=K;j++){
			if(sum+f[i-1][K-j]>=m){ a[n-i+1]=j+1,K-=j,m-=sum; break; }
			sum+=f[i-1][K-j];
		}
	}
	for(int i=n;i>=1;i--){
		for(int j=i+1;j<=n;j++){
			if(a[j]>=a[i]) a[j]++;
		}
	}
	for(int i=1;i<=n;i++) wt(" \n"[i==n],a[i]);
	return 0;
}

洛谷 P3676 小清新数据结构题

首先套路的维护一下点 $1​$ 的答案，这种树上问题长得就很像剖，直接树剖，接下来考虑修改，现在其实就是区间修改（修改点到根的子树大小都变了），区间维护值的平方和，这个可以用一个简单的线段树来维护好，具体来说：维护三个变量 $sum1,sum2,tag​$ 分别表示区间和，区间平方和和懒标记，$sum1​$ 是好修改的，考虑 $sum2​$ 怎么修改，其实就是 $\sum (val_u+k)^2=\sum {val_u}^2+2\times val_u \times k+k^2=(\sum {val_u}^2)+2\times sum1 \times k + len*k^2​$，其中 $k​$ 是区间修改的值，$len​$ 是区间长度，这个是好做的。

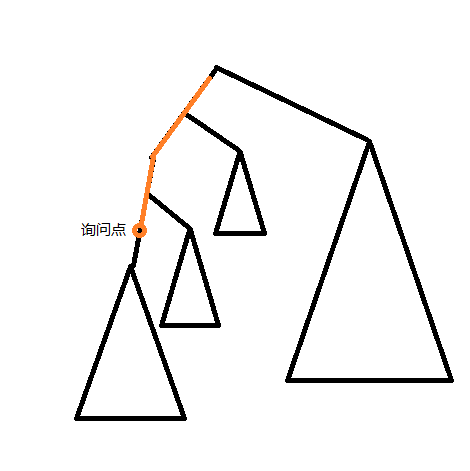
现在考虑换根，我们要对于每个点都能求出答案，发现只有根节点到询问点的链上的点权值会变，不懂的看下图就行了，应该还是挺明显的。

现在考虑一个在询问点到根节点的链上的点 $u$，他在链上的儿子是 $v$，他的权值会怎么变化，如果直接按照 $u$ 统计就是 $sum2$，而现在的贡献应该是 $\sum (size-sz_v)^2=cnt\times size^2-(\sum 2\times size\times sz_v)+cnt\times {sz_v}^2$，其中 $cnt$ 为询问点的深度减一（我这里根节点深度为 $1$，减一是因为特殊考虑询问点，即下面没有考虑询问点），$size$ 是根节点子树大小，这个柿子中 $size,cnt$ 是已知的，所以就只用考虑 $\sum sz_v$ 和 $\sum {sz_v}^2$ 了，不难发现这玩意就是询问点到根节点的儿子到询问点的 $sz$ 和（下图橙色段，注意上面没有顶到根节点），所以可以直接在线段树上查询。😁😁😁

然后考虑询问点，他的答案应该就是 $size^2​$，我们发现正好根节点的原先的答案没有被剪掉，并且他的值正好是 $size^2​$，所以直接不管就好了。

这样我们就做完了！😆😆😆

code

typedef long long LL;
const int N=2e5+7;
int n,m;
int a[N],b[N];
int dfn[N],nw[N],tot,top[N],fa[N],sz[N],son[N],dep[N];
vector<int>g[N];
inline void dfs1(int u,int FA){
	sz[u]=1,dep[u]=dep[FA]+1,fa[u]=FA;
	for(int v:g[u]){
		if(v==FA) continue;
		dfs1(v,u);
		sz[u]+=sz[v],a[u]+=a[v];
		if(sz[son[u]]<sz[v]) son[u]=v;
	}
}
inline void dfs2(int u,int TOP){
	top[u]=TOP,dfn[u]=++tot,nw[tot]=a[u];
	if(!son[u]) return ;
	dfs2(son[u],TOP);
	for(int v:g[u]){
		if(v==fa[u]||v==son[u]) continue;
		dfs2(v,v);
	}
}
LL sum1[N<<2],sum2[N<<2],tag[N<<2];
inline void change(int u,int len,int k){ sum2[u]+=2ll*sum1[u]*k+1ll*k*k*len,sum1[u]+=1ll*k*len,tag[u]+=k; }
inline void pushdown(int u,int l,int r){
	int mid=(l+r)>>1;
	change(u<<1,mid-l+1,tag[u]),change(u<<1|1,r-mid,tag[u]),tag[u]=0;
}
inline void pushup(int u){ sum1[u]=sum1[u<<1]+sum1[u<<1|1],sum2[u]=sum2[u<<1]+sum2[u<<1|1]; }
inline void build(int u,int l,int r){
	if(l==r) return sum1[u]=nw[l],sum2[u]=1ll*nw[l]*nw[l],void();
	int mid=(l+r)>>1;
	build(u<<1,l,mid),build(u<<1|1,mid+1,r);
	pushup(u);
}
inline void add(int u,int L,int R,int l,int r,int k){
	if(l<=L&&R<=r) return change(u,R-L+1,k),void();
	pushdown(u,L,R);
	int mid=(L+R)>>1;
	if(l<=mid) add(u<<1,L,mid,l,r,k);
	if(r>mid) add(u<<1|1,mid+1,R,l,r,k);
	pushup(u);
}
inline LL que(int u,int L,int R,int l,int r){
	if(l<=L&&R<=r) return sum1[u];
	pushdown(u,L,R);
	int mid=(L+R)>>1; LL ans=0;
	if(l<=mid) ans=que(u<<1,L,mid,l,r);
	if(r>mid) ans+=que(u<<1|1,mid+1,R,l,r);
	return ans;
}
inline void upd(int u,int k){ while(u) add(1,1,n,dfn[top[u]],dfn[u],k),u=fa[top[u]]; }
inline LL que(int u){ LL ans=0; while(u) ans+=que(1,1,n,dfn[top[u]!=1?top[u]:son[top[u]]],dfn[u]),u=fa[top[u]]; return ans; }
int main(){
	rd(n,m);
	for(int i=1;i<n;i++){
		int u,v; rd(u,v);
		g[u].eb(v),g[v].eb(u);
	}
	for(int i=1;i<=n;i++) rd(a[i]),b[i]=a[i];
	dfs1(1,0),dfs2(1,1);
	build(1,1,n);
	LL xzt=a[1];
	while(m--){
		int opt,u,k; rd(opt,u);
		if(opt==1) rd(k),upd(u,k-b[u]),xzt+=k-b[u],b[u]=k;
		else if(opt==2) wt('\n',sum2[1]-2*xzt*que(u)+1ll*xzt*xzt*(dep[u]-1));
	}
	return 0;
}

洛谷 P3673 小清新计数题

感觉是一道比较难的计数题，反正是我小丑了就对了。🤡👈🤣

首先 $n$ 个点 $n$ 条边并且每个点只有一条出边，这肯定是一个基环树森林。

将“第x句话为真”看成白边，“第x句话为假”看成黑边，考虑什么时候点击 Bad 时过关：

• 树：发现树上不管怎么赋边的颜色都不会点击 Bad，也就是树时可以随便填的。

• 环：环上的只能有偶树条黑边，原因是可以将白边缩起来，因为他们的状态是一样的，现在只剩一个有奇数条黑边的环，因为有奇环，所以根本能分配成”真，假，真，假…“这样。（感觉说的很不清楚😿，其实就是可以把黑边看成一个改变状态的边，我现在要是是真连出去之后就是假，这是一个类似二分图的东西，而奇环是肯定放不进去的，所以寄了）

有了这个性质，我们就很好 $dp$ 了，首先考虑一颗有 $x$ 条白边，$y$ 条黑边的基环树的个数，因为 $n$ 只有 $50$ 我们现在只有一个 $n^2$ 的状态，所以我们甚至可以直接枚举基环树的环上有 $a$ 条白边，$b$ 条黑边，然后我们现在要算的是

1. 一个长度为 $a+b$ 的环有多少种；
2. 将一个大小为 $a+b$ 的连通块和 $x+y-a-b$ 个大小为 $1$ 的连通块连起来的方案数。

上面的点都互不相同。

1. 因为点互不相同，所以可以重标号成排列，首先先算出一个长度为 $a+b$ 的排列列有多少种，这是个 🤡 东西，就是 $(a+b)!$，考虑变成环是什么样，发现我们直接除以 $a+b$ 就可以了，因为一个长度为 $i$ 的环会被统计 $i$ 次，比如"2,3,1,4"这个排列会在"2,3,1,4",“3,1,4,2”,“1,4,2,3”,"4,2,3,1"这里统计 $4$ 次，反正就是每个数开头都会被统计一次，所以直接环的数量就是 $(a+b-1)!$

2. 这个玩意就是 prüfer 序列，数量是 $(x+y)^{x+y-a-b-1}\times (a+b)$，证明在这里的最下面。

现在设 $f_{i,j}$ 表示一个有 $i$ 条白边，$j$ 条黑边的基环树的数量，有：

$$f_{i,j}=\sum\limits_{x=0}^{i}\sum\limits_{y=0\&2 \mid y}^{j} {i \choose x}{j \choose y}(x+y-1)!\times(i+j)^{i+j-x-y-1}\times (x+y)$$

这里 $y$ 要是二倍数是因为上面说的，环上的黑边必须是偶数条。

根据上面的解释，这个柿子是不是就变得很合理了 😆😆😆

但是这玩意还有个次方，还要再带个 $\log$，这就很烦！😔😔😔

但是你发现我统计的是基环树个数，这玩意跟边的颜色是没有关系的，所以我们可以再设一个 $g_{i,j}$ 表示一个有 $i+j$ 个点，环上点数是 $i$ 的基环树的方案数，根据上面的东西不难推出：

$$g_{i,j}=(i-1)!\times (i+j)^{j-1}\times i$$

注意到 $j$ 是可以取到 $0$ 的，所以要分讨一下，当 $j=0$ 时 $g_{i,j}=(i-1)!$

那么 $f​$ 的转移就改成了

$$f_{i,j}=\sum\limits_{x=0}^{i}\sum\limits_{y=0\&2 \mid y}^{j}{i \choose x}{j \choose y}g_{x+y,i+j-x-y}$$

接下来时统计答案，现在就是要把很多基环树频道一起，这个就套路很多了：😎

设 $h_{i,j}$ 表示一张有 $i$ 条白边，$j$ 条黑边的图的方案数，转移要注意避免算重，所以我们要钦定每次拿包含最小编号点的基环树（我是钦定白点编号小于黑点），即转移为：

$$\begin{aligned} \begin{cases} \sum\limits_{x=0}^{n-i}\sum\limits_{y=0}^{m-j}h_{i+x,j+y}\gets {n-i-1\choose x-1}{m-j\choose y} \times f_{x,y}\times h_{i,j} &(i\not=n)\\ \sum\limits_{y=0}^{m-j}h_{i,j+y}\gets{m-j-1\choose y-1} \times f_{0,y}\times h_{i,j} &(i=n) \end{cases} \end{aligned}$$

其中 $n$ 为白点数量，$m$ 为黑点数量，这样我们就做完了！😺😺😺

code

typedef long long LL;
const int P=998244353;
const int N=107;
int n,m;
char s[N];
int f[N][N],g[N][N],h[N][N];
int C[N][N],fac[N];
inline LL qmi(LL a,LL b,LL P){
	LL ans=1,x=a;
	while(b){
		if(b&1) ans=ans*x%P;
		x=x*x%P,b>>=1;
	}
	return ans;
}
inline void init(int n){
	fac[0]=1;
	for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%P;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=i;j++){
			if(!j) C[i][j]=1;
			else C[i][j]=(C[i-1][j]+C[i-1][j-1])%P;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=0;i+j<=n;j++){
			if(!j) g[i][j]=fac[i-1];
			else g[i][j]=1ll*fac[i-1]*i%P*qmi(i+j,j-1,P)%P;
		}
	}
}
int main(){
#ifndef ONLINE_JUDGE
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	rstr(s+1);
	for(int i=1;s[i];i++){
		if(s[i]=='1') n++;
		else m++;
	}
	init(n+m);
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			for(int x=0;x<=i;x++){
				for(int y=0;y<=j;y+=2){
					if(!(x+y)) continue;
					f[i][j]=(f[i][j]+1ll*C[i][x]*C[j][y]%P*g[x+y][i+j-x-y])%P;
				}
			}
		}
	}
	h[0][0]=1;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			if(n-i){
				for(int x=1;x<=n-i;x++){
					for(int y=0;y<=m-j;y++) h[i+x][j+y]=(h[i+x][j+y]+1ll*C[n-i-1][x-1]*C[m-j][y]%P*f[x][y]%P*h[i][j])%P;
				}
			}
			else{
				for(int y=1;y<=m-j;y++) h[i][j+y]=(h[i][j+y]+1ll*C[m-j-1][y-1]*f[0][y]%P*h[i][j])%P;
			}
		}
	}
	wt('\n',h[n][m]);
	return 0;
}