骨牌相关

🥰🥰🥰

今天做了两道骨牌题，感觉有点强，所以来摆了。😼😼😼

首先，骨牌是什么？

我也不知道

在题目里面好像就是一个大小为 $1\times2$ 的棋子（

有什么性质？

好像涉及骨牌的题还不少，比如说统计棋盘内放 $x$ 个骨牌的方案数，因为是 $1\times 2$ 的，所以直接状压有哪些位置突出来了就好了，当然也可以轮廓线（

以上均为口胡，不保证正确性😅😅😅

但是我现在不想写这个，这有一个更 👍 的性质：

首先假设你有一个棋盘，上面全部都是骨牌，只有一个空位，现在让你在不拿出骨牌的情况下在棋盘中滑动骨牌。（并且两种局面不同的区分方法是空位位置）

这玩意有什么性质呢，首先发现只有一个空位，所以我们可以把骨牌移动看成空位移动！

现在图就简单很多了，自会有一个会动的了。

那么空位的移动又有什么性质呢？

结论：空位的移动路径构成一颗树。

这是为什么呢？

首先我们将图奇偶黑白染色，发现空位只会在同种颜色中移动。

画个图就会发现这很正确：

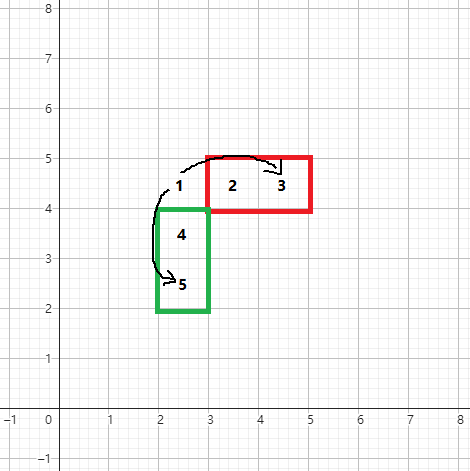
显然不管怎么走坐标都是 $\pm 2$，这肯定颜色不变。

现在图里面已经没有奇环了，现在我们要证明他没有偶环。

然后这玩意的证明非常蠢 😥😥😥，就是因为 $1\times2$ 的骨牌加上一个空位是奇数个位置，不可能有偶环（

现在就证明了这是一颗树了，这就很 🐂（这是牛） 了，很多问题就可以很简单的做出来了。

洛谷 P4701 粘骨牌

这玩意知道了上面的基本就是板子，首先将空位能到的所有点都 bfs 出来，然后考虑一个蠢到不能再蠢的树形 d(dáo)p：

设 $f_u$ 表示 $u$ 节点不能到任何特殊位置的最小代价，$val_u$ 为粘住 $u$ 节点所在骨牌的代价，转移也很蠢：$f_u=\min(val_u,\sum\limits_{v \in son(u)}f_v)$

这样我们就把这个题做完了！是不是非常简单 😸😸😸

code:

typedef pair<int,int> PII;
typedef long long LL;
const int N=1007;
const LL INF=1e18;
const int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
int n,m,K;
LL a[N*N];
int id[N][N]; bool st[N][N];
PII pos[N*N]; int cnt=0;
vector<int>g[N*N];
inline void bfs(){
	queue<int>q; q.push(1);
	while(q.size()){
		int xzt=q.front(); q.pop();
		int i=pos[xzt].first,j=pos[xzt].second;
		for(int k=0;k<4;k++){
			int x=i+dx[k],y=j+dy[k];
			if(x+dx[k]>0&&y+dy[k]>0&&x+dx[k]<=n&&y+dy[k]<=m&&id[x][y]==id[x+dx[k]][y+dy[k]]) pos[++cnt]={x+dx[k],y+dy[k]},g[xzt].eb(cnt),q.push(cnt);
		}
	}
}
LL f[N*N];
inline void dfs(int u){
	if(st[pos[u].first][pos[u].second]) f[u]=INF;
	for(int v:g[u]){
		dfs(v);
		f[u]+=f[v];
	}
	f[u]=min(f[u],a[id[pos[u].first][pos[u].second]]);
}
int main(){
	rd(n,m,K);
	a[0]=INF;
	for(int i=1;i<=(n*m-1)/2;i++) rd(a[i]);
	for(int i=1,x,y;i<=K;i++) rd(x,y),st[x][y]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			rd(id[i][j]);
			if(!id[i][j]) pos[++cnt]={i,j};
		}
	}
	if(st[pos[1].first][pos[1].second]) return puts("GG"),0;
	bfs(),dfs(1);
	wt('\n',f[1]);
	return 0;
}

CF1368G Shifting Dominoes

这个题就比上面那个题有意思多了。

首先还是建出上面说的那个树。（其实这里是森林，因为每个骨牌都有可能是起点 😆😆😆）

然后能发现我们这此建的树是单向边，不能走上去。

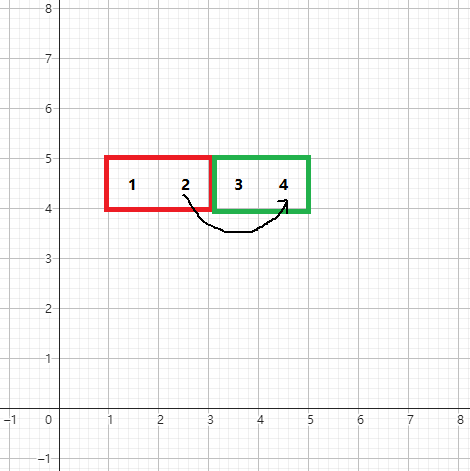
这里显然在拿掉绿色骨牌后 $4$ 是走不到 $2$ 的。

所以我们把树建出来后，答案就是两个骨牌在树上的子树大小乘起来的和！

吗？……

好像寄了 🤡👈🤣

为什么寄了呢？

刚才我们没有考虑两个空位路径的相交 🍌 问题，这显然是不能香蕉的。

首先竖着是没有事的：

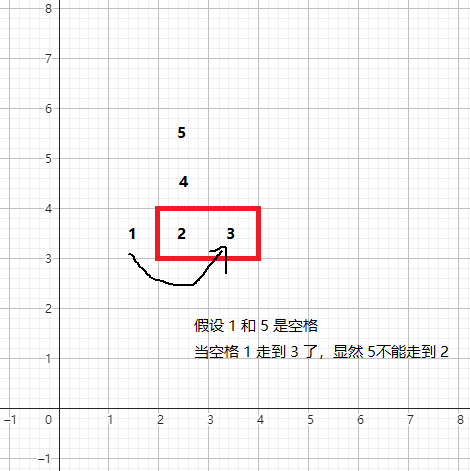
但是横着好像寄了：

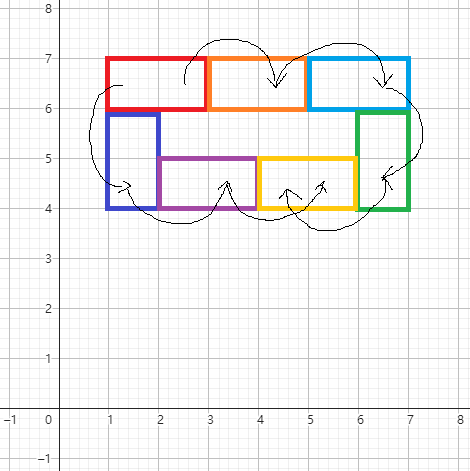
我们把红色骨牌拿走，然后按着箭头让他走就香蕉了 😣😣😣

不过我们现在先不管这个，这个一会自然就解决了。

根据刚才那个相交的启发（刚才那个其实等于直接拿掉黄色骨牌），现在有了一个更为致命的问题，我们算重了！

这样一个简单的情况我们就会寄，有我们会算出有 $4$ 中情况：（黑色为边界）

我们得想办法去重。

发现我们的答案其实是 $(黑色空位走到的位置，白色空位走到的位置)$，这玩意是二维的，那我们就把他放到二维上，将树按 $dfn$ 序重标号一下，现在我们拿掉一个骨牌可用的点就是一个矩形了，现在就是要求矩形面积并。

这玩意直接扫描线就好了，灰常简单！ 😛😛😛

哦对，上面还有那个重复的没说，你发现你将路径上相交的部分拿出来，他一定有一个完整骨牌，而且这个骨牌一定可以合法的走出上面那个不合法的情况，所以直接不用考虑了（比如上面那个就是直接拿掉黄色骨牌） 😄😄😄

code:

typedef long long LL;
typedef pair<int,int> PII;
const int N=2e5+7;
const int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
int n,m;
string s[N];
vector<int>id[N]; int js=0;
vector<bool>st[N];
vector<int>g[N];
int dfn[N],sz[N],tot=0;
bool flag[N],has[N];
inline int ID(int x,int y){ return (x-1)*m+y; }
inline void bfs(PII S){
	queue<PII>q; q.push(S);
	while(q.size()){
		PII A=q.front(); q.pop();
		int i=A.first,j=A.second;
		if(st[i][j]) continue;
		st[i][j]=1;
		for(int k=0;k<4;k++){
			int x=i+dx[k],y=j+dy[k];
			if(x+dx[k]>0&&y+dy[k]>0&&x+dx[k]<=n&&y+dy[k]<=m&&id[x][y]==id[x+dx[k]][y+dy[k]]) g[ID(i,j)].eb(ID(x+dx[k],y+dy[k])),q.push({x+dx[k],y+dy[k]}),has[ID(x+dx[k],y+dy[k])]=1;
		}
	}
}
inline void dfs(int u){
	flag[u]=1,dfn[u]=++tot,sz[u]=1;
	for(int v:g[u]) dfs(v),sz[u]+=sz[v];
}
struct segment{
	int l,r;
	segment(){ l=r=0; }
	segment(int L,int R){ l=L,r=R; }
};
vector<segment> add[N],del[N];
struct segmenttree{
	int tag[N<<4],sum[N<<4];
	inline void pushup(int u,int l,int r){
		if(tag[u]) sum[u]=r-l+1;
		else sum[u]=sum[u<<1]+sum[u<<1|1];
	}
	inline void upd(int u,int L,int R,int l,int r,int k){
		if(l<=L&&R<=r) return tag[u]+=k,pushup(u,L,R),void();
		int mid=(L+R)>>1;
		if(l<=mid) upd(u<<1,L,mid,l,r,k);
		if(r>mid) upd(u<<1|1,mid+1,R,l,r,k);
		pushup(u,L,R);
	}
}tr;
inline LL que(){
	LL ans=0;
	for(int i=1;i<=tot;i++){
		for(segment A:del[i]) tr.upd(1,1,tot,A.l,A.r,-1);
		for(segment A:add[i]) tr.upd(1,1,tot,A.l,A.r,1);
		ans+=tr.sum[1];
	}
	return ans;
}
int main(){
	rd(n,m);
	for(int i=1;i<=n;i++) rstr(s[i]),s[i]=" "+s[i];
	for(int i=0;i<=n+1;i++) id[i].resize(m+2),st[i].resize(m+1);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(s[i][j]=='U') id[i][j]=id[i+1][j]=++js;
			if(s[i][j]=='L') id[i][j]=id[i][j+1]=++js;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(st[i][j]) continue;
			bfs({i,j});
		}
	}
	for(int i=1;i<=n*m;i++) if(!has[i]) dfs(i);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(s[i][j]!='U'&&s[i][j]!='L') continue;
			int l=dfn[ID(i,j)],r=dfn[ID(i,j)]+sz[ID(i,j)]-1,L,R;
			if(id[i][j]==id[i][j+1]) L=dfn[ID(i,j+1)],R=dfn[ID(i,j+1)]+sz[ID(i,j+1)]-1;
			else L=dfn[ID(i+1,j)],R=dfn[ID(i+1,j)]+sz[ID(i+1,j)]-1;
			if((i+j)&1) swap(l,L),swap(r,R);
			add[l].eb(segment(L,R)),del[r+1].eb(segment(L,R));
		}
	}
	wt('\n',que());
	return 0;
}