推柿子题
x∑P−1y∑P−1∃n∈N xn≡y(modP)
1+x=1∑P−1y=1∑P−1∃n∈N xn≡y(modP)
考虑模 P 意义下的原根 g ,有 x=ga,y=gb
1+x=1∑P−1y=1∑P−1gan≡gb(modP)
1+x=1∑P−1y=1∑P−1an≡b(modP−1)
这个可以看成一个长度为 P−1 的环,我每次在上面走 a 步,求 b 的数量,这个是 gcd(a,P−1)P−1 个。
1+a=1∑P−1gcd(a,P−1)P−1
1+d∣(P−1)∑dP−1a=1∑P−1[gcd(a,P−1)=d]
1+d∣(P−1)∑dP−1φ(dP−1)
现在就可以求了
1e12 以内的约数数最多的数有 6720 个约数,跑不满
code
可以说只要会 FWT 就可以切
题意:给定长度为 K 的数组 A ,给定 N ,现在你要选择有 [1,N] 堆石子,每一堆石子的数量 ∈A ,现在玩 nim 游戏,求先手获胜的局面有多少种
其实就是满足在 xa×xb=xa xor b 下求 [xt]i=1∑n(f(x))i 其中 t∈[1,值域]
因为 FWT(A+B)=FWT(A)+FWT(B),FWT(A xor B)=FWT(A)×FWT(B)
所以可以首先先 FWT,然后对 FWT 的每一项做 i=1∑naxi=a−1axn+1−a,然后 IFWT
code
小清新计数题
看数据范围考虑状压
设 fS 表示现在与一联通的子图点集是 S 的方案数,转移发现不好转移,所以正难则反,用总数减去不合法
code(这里 f 为了卡常没有点 1
个人感觉非常困难
详细写了题解
洛谷题解全是扯淡的
首先发现可以直接建图流,但是这样时间复杂度是 O(nmk) 的,%114514 过不了,考虑优化
发现有一个东西是 Dijsktra 求最小费用流,时间复杂度是 O(nm+kmlogm) 的,时间复杂度瓶颈在一开始要求一遍 spfa ,考虑怎么建出来图没有负权边,之前的建图要建负权边是因为我要求的是最大费用最大流,发现这玩意就是最小浪费代价最大流,这玩意要怎么弄呢,首先缩点成为一个 dag ,按 dag 层数标号,我要是从一个编号为 i 的点到一个编号为 j 点的话中间的肯定选不上,要是走到这里就不走了说明后面的全选不了,这样就可以做了
code
挺傻逼的一道题
但是我降智没想出来/ng
退役算了/cf
假设现在有 m 种颜色,你选 x 个球,那么选颜色 i 的概率就是 (xn)(xn)−(xn−sumi)
这样就可以 O(n2) 了
然后发现本质不同的 sumi 个数时 n 级别的,所以可以 O(nn) 做了
学习到的很多
很容易联想到二分图,每一个球是左部点,每一个盒子是右部点(当然做的时候不用建出来,不然就寄了,所以下面说的左部点都是对于颜色,右部点都是对于盒子),求完美匹配
考虑霍尔定理
n<=20 可以直接枚举,但是发现右部点的权值不好算,所以可以改一下枚举的定义,即我选了一些右部点,他们所有可达的左部点集合为 S ,这样就可以 FWT 算右部点权值了
假设现在我选的左部点权值是 x ,右部点权值是 y ,第一问答案就是 cnt=min{y−x+1}
将不用删点特判掉之后考虑求方案数
当一个左部点集合 S 删去 cnt 个点时没有完美匹配当且仅当 ∃ T S∈T 且 T 的 y−x+1=cnt ,为了不算重,我们钦定 S 里面包含的颜色都至少被删去一个球。
至于怎么求,考虑容斥
先提前算出不钦定的值,然后外层枚举现在处理到第几个颜色,内层枚举集合 S 现在等于时颜色编号小于 S 的都已经钦定选了,然后你减去把现在枚举的颜色去掉的 dp 值,仔细想想发现很正确
code
可能?是套路题
但是我不会/ng
因为我不能记时间,所以可以考虑费用提前计算
首先先思考假如蜡烛可以燃烧到负数,发现这就是 P1220 关路灯 ,但是现在不能燃烧到负数,也就是 max(0,ai) ,于是就有一个思路就是在第 i 根蜡烛的时候把 ai 和 0 都转移一遍,因为是取 max ,所以最后答案是正确的
现在我不知道有多少蜡烛是没到就会燃尽,所以我区间 dp 多记一维表示当前区间外有 i 根蜡烛未燃尽,这样就可以实现上述转移了
设 fl,r,i,0/1 表示在区间 [l,r] ,区间外有 i 根蜡烛在燃烧,现在在 左/右 端点时的燃烧掉的最小值
fl,r+1,i,0=min{fl,r,i,0/1+i×dist+ar+1,fl,r,i+1,0/1+i×dist} 其他转移同理
min 中前面的就是 r+1 的熄灭了,后面的时没熄灭的
code
糗大了,做法是个傻逼玩意
直接推柿子。
题目要求:
i=1∑nj=i∑n[gcd(i,j)=1][gcd(Pi,Pj)=1]
有 gcd ,考虑莫比乌斯反演,发现莫比乌斯反演好像只能做 gcd(i,j)=1 ,所以先推一下 i=1∑nj=i∑n[gcd(i,j)=1][gcd(Pi,Pj)=1] 其实是我一开始看错题了。
首先将 [gcd(i,j)=1] 莫比乌斯反演一下:
\begin{eqnarray}
&\sum_{i=1}^{n}&\sum_{j=i}^{n}[\gcd(i,j)=1][\gcd(P_i,P_j)=1] \\
=&\sum_{d=1}^{n}&\mu(d)\sum_{d\mid i}^{n}\sum_{d\mid j}^{n}[\gcd(P_i,P_j)=1][i \le j] \\
\end{eqnarray}
然后将 [gcd(Pi,Pj)=1] 反演一下:
\begin{eqnarray}
&\sum_{d=1}^{n}&\mu(d)\sum_{k=1}^{n}\mu(k)\sum_{d\mid i,k\mid P_i}^{n}\sum_{d\mid j,k \mid P_j}^{n}[i \le j] \\
=&\sum_{d=1}^{n}&\mu(d)\sum_{k=1}^{n}\mu(k)\ \frac{sum(d,k) (sum(d,k)+1)}{2} \\
\end{eqnarray}
其中 sum(d,k) 表示 d∣i,k∣Pi 的 i 的个数。
不难发现对于每一个数 i 最多只会对 sum 数组贡献 log2 次,因为约数个数是 log 级别的,所以时间复杂度 O(nlog2n)。
现在已经会做 i=1∑nj=i∑n[gcd(i,j)=1][gcd(Pi,Pj)=1] ,考虑怎么转化回题目本身,考虑莫比乌斯反演的本质是依靠 d∣n∑μ(d)=[n=1] 这个柿子搞的,现在我们要求的是跟这个正好相反的柿子,也就是说只要构造出来一个函数 ξ(i) 满足 d∣n∑ξ(d)=[n=1] 就可以了,这个很好构造,考虑 μ 的定义:
μ(i)=⎩⎨⎧1n=10 i 含有质因子平方(−1)k k 为 i 的质因子个数
首先因为 n=1 时要求 ξ(n)=0 ,所以:
ξ(i)={0n=1
然后考虑为什么当 n=1 时 μ(i)=0 ,假设 n 有 k 个质因子,根据定义 d∣n∑nμ(d)=i=0∑k(−1)i(ik) ,因为有平方因子贡献为 0 ,所以直接枚举有几个因子就可以了。
把平方质因子搞掉这个性质很好,我们可以借鉴过来,也就是我们还是不要平方因子,现在的规则就是:
ξ(i)={0n=10 i 含有平方因子
现在就是只要构造出 fi 满足 i=1∑kfi(ik)=1 就可以了,还是借鉴莫比乌斯函数,发现 i=1∑k(−1)k(ik)=−1 ,所以我们直接取反就好了。
也就是现在的规则是:
ξ(i)=⎩⎨⎧0n=10 i 含有质因子平方(−1)k−1 k 为 i 的质因子个数
现在我们已经构造出 ξ 了,只要将上面推出来的柿子中的 μ 换成 ξ 就好了。
code
挺神秘的一道题
题意:给你一棵树,多次询问,每次询问给定两个点 x,y,求 u=1∑nmin(dist(u,x),dist(u,y))
如果只有一个点发现非常好求,直接换根 dp 就好了,现在考虑两个点怎么做
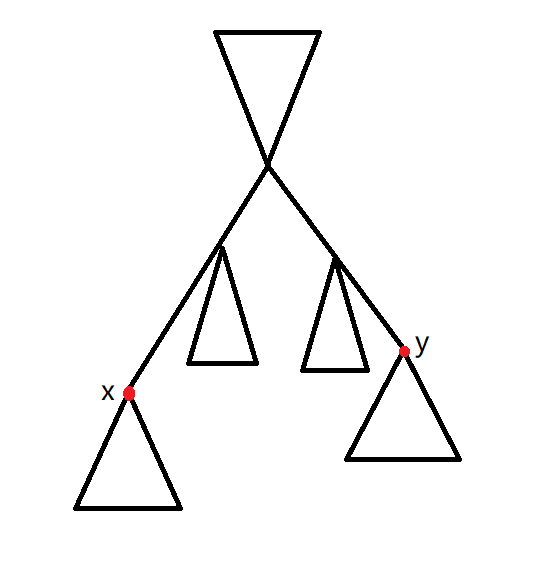
首先肯定是要找出 u 到 v 的中点 mid 的
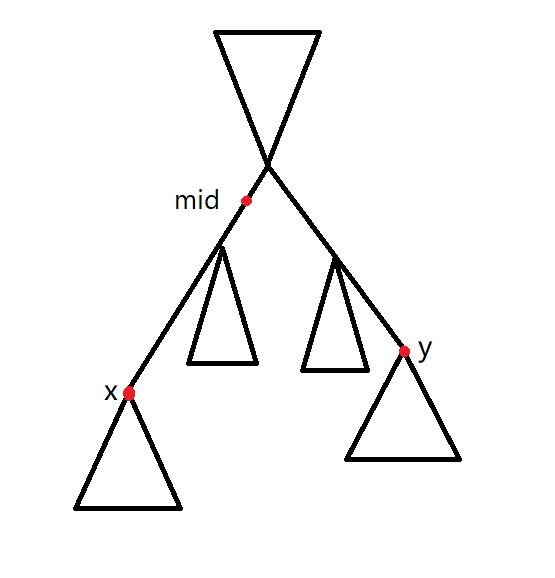
其中以 mid 为子树的点肯定是到 u , 而剩下的节点是到 v
现在把式子列出来:
设集合 S 包含以 mid 为子树的的节点(黄色方框包含的节点),集合 T 包含剩下的节点(绿色方框包含的节点)
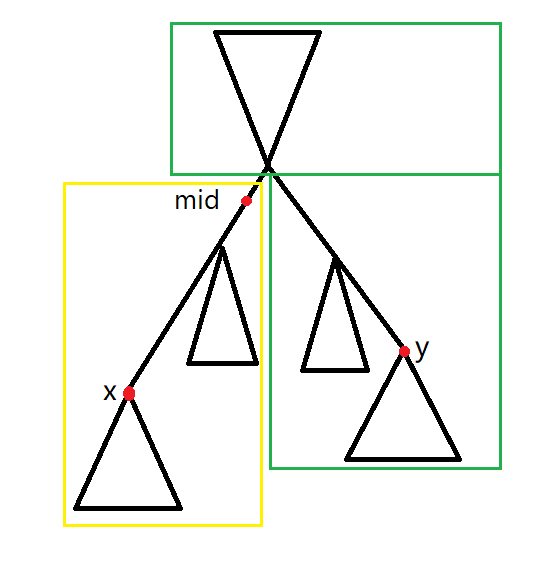
ans=u∈S∑dist(u,x)+u∈T∑dist(u,y)
ans=u=1∑n(dist(u,x)+dist(u,y))−(u∈S∑dist(u,y)+u∈T∑dist(u,x))
ans=u=1∑n(dist(u,x)+dist(u,y))−(u∈S∑dist(u,mid)+u∈T∑dist(u,mid)+szmid×dist(mid,y)+(n−szmid)×dist(mid,x))
ans=u=1∑n(dist(u,x)+dist(u,y)−dist(u,mid))−szmid×dist(mid,y)−(n−szmid)×dist(mid,x))
哈哈,非常神奇的我们就可以做了
时间复杂度 O(nlogn)


