线性代数学习笔记

注：除了上面那张图都是贺的 $\text{3Blue1Brown}$ 的

向量

向量可以是任何东西，只要保证两个向量相加以及数字与向量相乘是有意义的即可

向量加法：

$\vec{v}+\vec{w}$ 如图：

为什么是这样定义的？

可以将向量看成一种特定的运动，即在空间中按照向量方向走他的长度的距离，这样定义加法时走 $\vec{v}$ 和走 $\vec{w}$ 是等同于走 $\vec{v}+\vec{w}$ 的

考虑矩阵

$$\begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} a \\ b \end{bmatrix}$$

等于先沿纵坐标方向走 $x$ 距离，然后沿横坐标方向走 $y$ 距离，沿纵坐标方向走 $a$ 距离，然后沿横坐标方向走 $b$ 距离，所以上面两个矩阵加完就是

$$\begin{bmatrix} x+a \\ y+b \end{bmatrix}$$

向量数乘：

$a\vec{x}$ 等于把向量 $x$ 拉长 $a$ 倍

这种过程被称为缩放 $a$ 被称为标量，在线性代数中数字的主要作用就是缩放向量

$$a \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a\times x \\ b\times y \end{bmatrix}$$

矩阵

$$\begin{bmatrix} x \\ y \end{bmatrix}$$

可以表示为 $x\times \hat{i}+y \times \hat{j}$

$$\hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} ,\hat{j}= \begin{bmatrix} 0 \\ 1 \end{bmatrix}$$

$\hat{i}$ 与 $\hat{j}$ 是 $xy$ 坐标系的基向量

当然基向量也可以不选这俩，只要不共线就行了

当用数字描述向量时，都依赖于正在使用的基

$a\vec{v}+b\vec{w}$ 被称为两个向量的线性组合

为啥叫线性组合？

将一个标量固定，发现这两个向量加起来后产生的向量的终点在一条直线上（$3B1B$ 这样说的

将两个标量同时改变，如果不共线则可以组合出所有二维平面中的向量，但是共线时时一条直线

所有可以表示为给定向量线性组合的向量构成的集合被称为给定向量张成的空间($\text{span}$)

向量与点：通常用向量的终点代表该向量

三维空间中的张成空间

两个三维向量张成的空间是一个二维平面

那当加上第三个向量呢？

线性组合的定义是很像的 $a\vec{v}+b\vec{w}+c\vec{u}$

如果第三个向量落在了前两个向量的平面上，那就还是在这个平面上否则能得到所有三维向量

更高维的我不会了，可以让 [$sls$] 帮你想一下

要是有多个向量，并且可以在不改变张成空间大小的情况下移除一些向量，则称这些向量是线性相关的

另一种表述是其中一个向量可以被表示为其他向量的线性组合

否则就是线性无关的了

向量空间的一组基是张成该空间的一个线性无关向量集

矩阵与线性变换

变换：就是函数的一个其他叫法，输入一些东西，输出所对应的东西，在线性代数中考虑的是向量输入输出

为什么叫变换不叫函数？就是暗示可以通过特定方式来可视化变换关系

线性代数限制在了一种特殊的变换上，线性变换

线性变换性质：

1. 直线变换后仍为直线
2. 原点必须保持固定

可以把线性变换看作“保持网格线平行且等距分别“的变换

你只要知道 $\hat{i}$ 和 $\hat{j}$ 变换后的位置就能求出所有向量了，因为这俩是 $2d$ 平面一组基

也就是一个二维线性变换可以仅由 $4$ 个数字确定，即变换后 $\hat{i}$ 的向量和 $\hat{j}$ 的向量

将他们写成矩阵

$$\begin{bmatrix} a&b\\ c&d \end{bmatrix} \\ 其中 \begin{bmatrix} a\\ c \end{bmatrix} 是变换后的 \hat{i} ， \begin{bmatrix} b\\ d \end{bmatrix} 是变换后的 \hat{j}$$

线性变换对矩阵的作用就直接按照矩阵乘法乘起来就好了

$$所以对于向量 \begin{bmatrix} x\\ y \end{bmatrix} 的变换就是 \\ \begin{bmatrix} a&b\\ c&d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = x \begin{bmatrix} a\\ c \end{bmatrix} + y \begin{bmatrix} b\\ d \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy \end{bmatrix}$$

矩阵乘法与线性变换复合

假设我要进行两个线性变换，这玩意叫“复合变换”

假设现在做两个线性变换

$$\begin{bmatrix} a&b \\ c&d \end{bmatrix} \begin{bmatrix} e&f\\ g&h \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}$$

$$你是先将 \begin{bmatrix} x\\ y \end{bmatrix} 乘上 \begin{bmatrix} e&f\\ g&h \end{bmatrix} 然后再乘上 \begin{bmatrix} a&b \\ c&d \end{bmatrix}$$

这是因为函数 $f(g(x))$ 这类的也是先看里面，道理相似

为什么矩乘没有交换律：

代数就不证了，懒得写

可以画个图看看嘛反正不是我画的：

先剪切后逆时针 $90^{\circ}$

先逆时针旋转 $90^{\circ}$ 后剪切

寄！

为什么矩阵乘法有交换律：

你考虑

$ABC$ 和 $(AB)C$ ，从右往左读没有任何区别

所以就证完了（雾

行列式

在进行线性变换时改变面积的比例被称为这个线性变换的行列式

比如：

变换到

这个线性变换的行列式就是 $2$

如果这个线性变换将原来的空间缩小了，则行列式为 $0$ ，比如将一个二维平面压成一条直线

如果空间定向发生了改变，则行列式为负

什么是定向？

就比如二维平面，可以将二维平面看成一张纸，将纸的正反面改变，定向就发生了改变，在二维平面中，一开始 $\hat{j}$ 在 $\hat{i}$ 的逆时针方向，如果在进行变换后到了 $\hat{i}$ 的顺时针方向，就等于定向发生改变

这个线性变换的行列式就是 $-3$ （图好像寄了）

为什么空间定向变化后行列式为负？

考虑随着 $\hat{i}$ 和 $\hat{j}$ 靠近时面积的变化比例，他会慢慢接近于 $0$ ，当 $\hat{i}$ 与 $\hat{j}$ 重合时行列式为 $0$ ，所以继续走下去行列式为负数就变得合理了

但是上面所说的都是在二维空间下，那么三维呢

也是缩放的比例，不过变成了缩放体积的比例

那么三维空间中行列式为负怎么判断呀

有一个右手定则

如果 $\hat{i},\hat{j},\hat{k}$ 能和手这样匹配上行列式就为正，否则为负

怎么计算行列式？

$$对于一个 2 \times 2 的矩阵 \begin{bmatrix} a&b \\ c&d \end{bmatrix} 他的行列式 \det \begin{pmatrix} \begin{bmatrix} a&b \\ c&d \end{bmatrix} \end{pmatrix} =ad-bc$$

大概理解一下的话就是先假设 $b,c$ 都为 $0$ ， $a,d$ 就是表示 $\hat{i},\hat{j}$ 的缩放面积，当 $b,c$ 有一项不为 $0$ 时这是一个平行四边形，面积还是 $ad$ ，但是要是两个都不为 $0$ ， $bc​$ 项会告诉你平行四边形在对角方向上变化了多少

具体的证明就是这个

那么三阶行列式呢

$$\det \begin{pmatrix} \begin{bmatrix} a&b&c \\ d&e&f \\ g&h&i \end{bmatrix} \end{pmatrix} = a \det \begin{pmatrix} \begin{bmatrix} e&f \\ h&i \end{bmatrix} \end{pmatrix} -b \det \begin{pmatrix} \begin{bmatrix} d&f \\ g&i \end{bmatrix} \end{pmatrix} +c \det \begin{pmatrix} \begin{bmatrix} d&e \\ g&h \end{bmatrix} \end{pmatrix}$$

但是这些在 $OI$ 中好像都没有用

所以 $n$ 阶行列式怎么求值呢？

设 $A$ 为一个 $n$ 维空间中的变换

$\det(A)=\sum\limits_p (-1)^{\tau(p)}\prod\limits_{i=1}^n A_{i,p_i}$ 其中 $p$ 是一个排列，$\tau(p)$ 是 $p$ 的逆序对数，这样直接算是 $O(n!\ n\log n)$

一些定义：

• 当 $2 \not\mid \tau(p)$ 为奇排列，否则为偶排列
• 将一个排列交换两个元素位置被称为对换，发生一次对换后排列奇偶性发生改变（画一下就明白了）

所以直接做直接寄，既然不能直接做，那么就肯定要找一些性质了

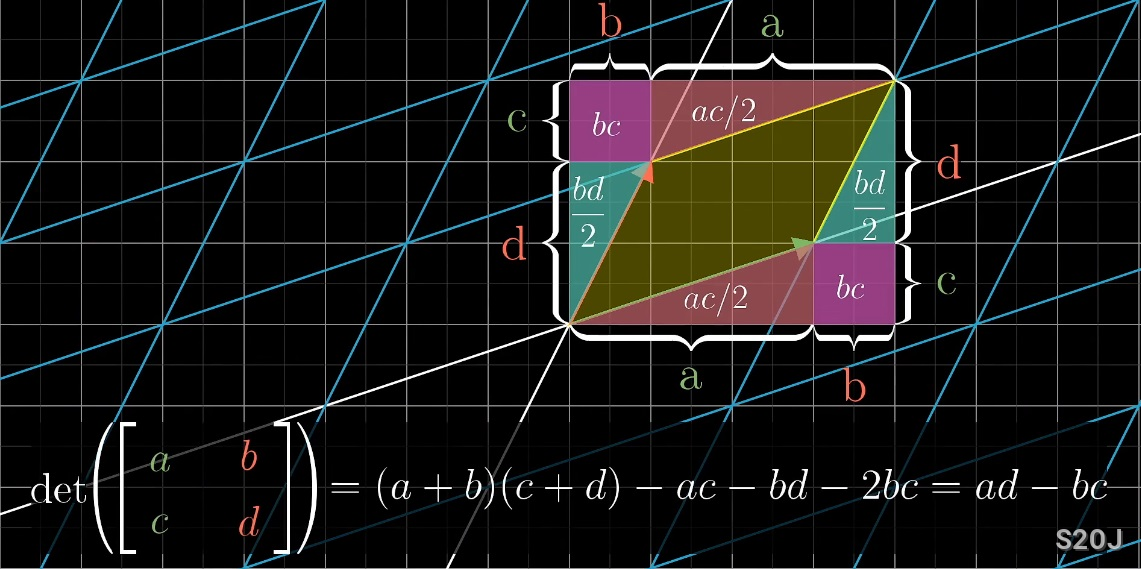
1. 交换 $A$ 的两行/列，行列式取反

   证明：我们不考虑换$A$ ，考虑换 $p$ 的两个位置，这玩意等于就是在算 $\tau(p)$ 的时候不交换，但是在弄 $A_{i,p_i}$ 时交换，这显然是正确的，因为一次对换后奇偶性发生改变，所以时相反数

2. $A$ 的行/列所有元素等比例变化，则行列式也等比例变化（这是显然的）

   $$\det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ k\times a_{x,1}&k\times a_{x,2}&\cdots&k\times a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} = k\times \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix}$$

3. 如果矩阵 $A$ 中有一行/列，是对应 $2$ 个矩阵 $B,C$ 中分别的 $2$ 相同位置的行/列所有元素之和。那么有 $\det(A)=\det(B)+\det(C)$ （也是显然的）

   $$\det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ b_{x,1}+c_{x,1}&b_{x,2}+c_{x,2}&\cdots&b_{x,n}+c_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} = \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ b_{x,1}&b_{x,2}&\cdots&b_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} + \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ c_{x,1}&c_{x,2}&\cdots&c_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix}$$

4. 如果 $A$ 存在两行/列成比例则 $\det(A)=0$

   $$\det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ k\times a_{x,1}&k\times a_{x,2}&\cdots&k\times a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} =0$$

   证明：对于排列 $p$ 做一个第 $x$ 行和第 $y$ 行的变换，发现行列式互为相反数，所以为 $0$ ，列同理

5. 把 $A$ 的一行/列的值全部乘一个常数加到另一行/列上，行列式值不变

   $$\det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{y,1}&a_{y,2}&\cdots&a_{y,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} = \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ k\times a_{x,1}+a_{y,1}&k\times a_{x,2}+a_{y,2}&\cdots&k\times a_{x,n}+a_{y,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix}$$

   证明：将后面那个矩阵用性质 $3$ 拆开，有

   $$\det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{y,1}&a_{y,2}&\cdots&a_{y,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} = \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{y,1}&a_{y,2}&\cdots&a_{y,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix} + \det \begin{pmatrix} \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n} \\ a_{2,1}&a_{2,2}&\cdots&a_{2,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{x,1}&a_{x,2}&\cdots&a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ k\times a_{x,1}&k\times a_{x,2}&\cdots&k\times a_{x,n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&a_{n-1,n} \\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \\ \end{bmatrix} \end{pmatrix}$$

   由性质 $4$ 可得，最后那个矩阵的行列式为 $0$

有了这些性质就可以快速求行列式了 😍😍😍

发现要是矩阵中要是有一项 $A_{x,y}$ 为 $0$ 的话，对行列式的改变其实时很大的，所有 $p_x=y$ 的都不用算了，快算行列式的方法就是通过上面所说的一些性质变化出来 $0$

发现上面所有的变换跟高斯消元巨像，所以就直接高斯消元就好了，发现最后一定会消成一个上三角矩阵，所以排列 $p$ 就只有唯一一种取法了，时间复杂度 $O(n^3)$

P7112 【模板】行列式求值

这道题很傻逼，模数不一定是质数，所以现在没有除法操作了 😡😡😡 ，那怎么办呢，发现好像可以辗转相减，对于 $a,b$ 要是 $a>b$ 就让 $a$ 减去 $b$ ，否则 $b$ 减去 $a$ ，不难发现这样最后 $b$ 一定会变成 $0$ 的。

但是这样是 $O(n^3\log n)$ 的， $n=600$ 直接寄，怎么办呢？你发现每次辗转相减两次 $A_{i,i}$ 是会缩小为原来的 $\frac{1}{2}$ 的，所以只会辗转相减 $O(n\log n)$ 次，每次 $O(n)$ ，时间复杂度 $O(n^3+n^2\log n)$

code

逆矩阵，列空间，零空间

线性方程组可以通过矩阵来表示

例如：

$$2x+5y+3z=-3 \\ 4x+0y+8z=0 \\ 1x+3y+0z=2$$

可以写成

$$\begin{bmatrix} 2&5&3 \\ 4&0&8 \\ 1&3&0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 0 \\ 2 \end{bmatrix}$$

现在我们就等于要寻找一个向量 $\vec{v}$ 变换后与 $\vec{w}$ 重合

假设现在你有一个方程 $A\vec{v}=\vec{w}$

当行列式不为 $0$ 时

可以通过一个逆向操作的变换将 $\vec{w}$ 变成 $\vec{v}$

这个逆向操作的变换被称为 $A$ 的逆，记为 $A^{-1}$

$A^{-1}$ 的核心性质在于他乘上 $A$ 等于什么也没有干，这个被称为恒等变换

当求完逆后,就有

$A^{-1}A\vec{v}=A^{-1}\vec{w}$

$\vec{v}=A^{-1}\vec{w}$

当行列式不为 $0$ 时一定有逆变换

当行列式为 $0$ 时就没有逆变换了，但是不一定无解，如果答案正好在压成的空间上也是有解的

拿三维空间举例，显然变换成一个平面比变换成一条直线更容易有解，所以就有了新的定义秩，变换后时几位空间变换的秩就是几

变换后是所有能输出的向量的集合被称为矩阵的列空间，也就是 $\{A\vec{v}\}$ ，为什么叫列空间呢？因为这是把矩阵每一列拉出来当成向量构成的张成空间，所以更精确的秩的定义是列空间的维数

当秩达到最大值时，意味着秩和列数相同，这个被称为满秩

$$\begin{bmatrix} 0 \\ 0 \end{bmatrix} 一定在 列空间里，因为线性变换原点不变$$

对于一个满秩变换来说，零向量是唯一变换后还在本身的

遂于一个非满秩变换来说，会有一定向量在变换后变为零向量，变换后落在原点的向量集合被称为矩阵的**“零空间”或“核”**

矩阵求逆

因为是学 $OI$ 的，所以还是要学怎么求 😔😔😔

不过还好很简单！

已知 $A\times A^{-1}=I$

那么我们让 $A$ 和一个单位矩阵拼起来，拼成 $[AI]$

现在让他乘就是 $A^{-1}\times [AI]=[IA^{-1}]$

所以把 $[AI]$ 的左边消成单位矩阵，用高斯消元即可

非方阵

非方阵是什么呢？一个 $n\times m$ 的矩阵可以理解为将 $m$ 维空间中的向量转换为 $n$ 维空间的向量

点积与对偶性

点积

$$\begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ … \\ b_{n-1} \\ a_n \\ \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ … \\ b_{n-1} \\ b_n \\ \end{bmatrix} =\sum\limits_{i=1}^{n} a_i\times b_i$$

在二维平面中，这个玩意同样等于 $\vec{v}\vec{w}\cos\alpha$ ，其中 $\alpha$ 是 $\vec{v}$ 和 $\vec{w}$ 的夹角

为什么点积与顺序无关？

直观来讲，首先如果向量长度相同，发现对称，这是一样的

现在将 $\vec{v}$ 缩放为 $k\vec{v}$，就没有对称性了 😔

但是可以这样想，如果是将 $\vec{w}$ 投影到 $k\vec{v}$ 上，$\vec{w}$ 的投影长度肯定是不变的，所以是 $k\vec{v}\vec{w}$

要是将 $k\vec{v}$ 投影到 $\vec{w}$ 上，等于是投影长度伸长了 $k$ 倍，所以也是 $k\vec{v}\vec{w}$