
除了上面这张图都是贺的一数的
正弦:sin ,余弦:cos ,正切:tan ,余切:cot ,正割:sec ,余割:csc
任意角三角函数:在平面直角坐标系上画一个单位圆,角 α 作为角度,边按照三角函数规则比起来就是任意角三角函数,与圆相连的是斜边,对边就是对边,临边就是临边
同角三角函数的基本关系
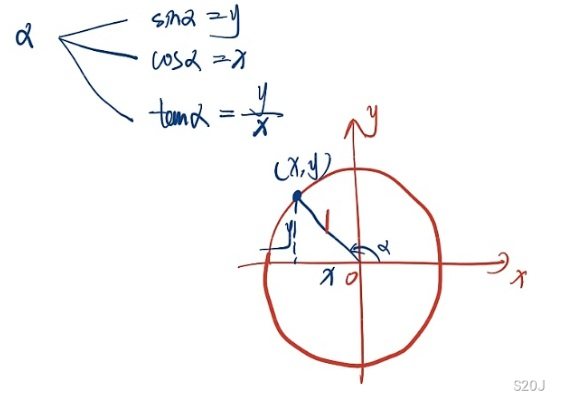
首先有 x2+y2=1
- cos2α+sin2α=1
- tanα=cosαsinα 注意 cosα 不能等于 0 ,即 α=2π+kπ,k∈Z
诱导公式
这里只用证明第一象限是正确的就可以推广到所有象限了
y=sinα 是奇函数
y=cosα 是偶函数
y=tanα 是奇函数
画个单位圆就出来了
sin(2π−α)=cosα 这两个角互余
cos(2π−α)=sinα 同理
tan(2π−α)=cotα 定义
sin(π−α)=sinα
cos(π−α)=−cos(α)
tan(π−α)=−tan(α)
奇变偶不变,符号看象限
sin(α+k2π),sin(α+k2π)
当 k 为奇数的时候 sin(cos) 变为 cos(sin)
将 kmod4 后看原来三角函数正负值
sin(α−23π)=sin(α+(−3)2π)=cosα
cos(27π−α)=cos(α−23π)=−sinα 第一部转化是因为是偶函数
三角恒等变换
三角函数和与差公式
研究多个角之间的关系
sin(α+β)=sinαcosβ+cosαsinβ
sin(α+β)=sinαcosβ−cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβ
tan(α+β)=1−tanαtanβtanα+tanβ
tan(α+β)=1+tanαtanβtanα−tanβ
后面柿子的符号可以通过角的大小变化来记
辅助角公式
sinα+cosα=2(sinα21+cosα21)
因为 sin45∘=cos45∘=21
所以原式等于 2(sinαcos45∘+cosαsin45∘)=2sin(α+45∘)
推广:
Asinα+Bcosα=A2+B2(sinαA2+B2A+cosαA2+B2B)
发现一定可以找到一个角 β 使得 cosβ=A2+B2A,sinβ=A2+B2B
所以原始等于 A2+B2sin(α+β)
二倍角公式
我们知道 sin(α+β)=sinαcosβ+cosαsinβ ,所以当 α=β 时 sin2α=2sinαcosα
同理 cos2α=cos2α−sin2α
因为 sin2α+cos2α=1 ,所以 cos2α=2cos2α−1 ,同理,也有 cos2α=1−2sin2α ,这玩意是可以降次的
tan2α=1−tan2α2tanα
解三角形
正弦定理
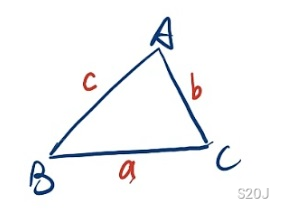
sinAa=sinBb=sinCc=2R,R 是外接圆半径
证明:作垂线就行了,2R 就做一个这个就好了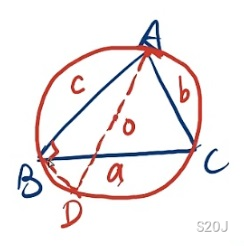
余弦定理
c2=a2+b2−2abcosC
推论:cosC=2aba2+b2−c2
证明:设向量 AB 为 c ,向量 CB 为 a 向量 CA 为 b
有 c=a−b
c2=(a+b)2
c2=a2+b2+2ab
c2=a2+b2+2abcosC




